A new preprint with Shunhao Oh and Dana Randall explains how to program simple computational “particles” of different types to self-organize into corresponding spatial regions that have a given hierarchical structure. The size, shape, and hierarchy of the regions are determined by the particles’ densities and affinities for particles of different types. Proving that the algorithm works requires new techniques for analyzing the Gibbs distributions of fixed-magnetization models from equilibrium statistical mechanics.

You can read the preprint here.

Examples of hierarchical sorting 🔗

If you’d like to know where the connection between programmable matter and statistical mechanics comes from, read on. But, first, some examples of hierarchical sorting from the paper. Here, “types” of particles are represented by colors. The first figure features eight types of particles, while the second features nine types. I defer to the preprint for an explanation of the interactions between colors that lead to these hierarchical sorts.

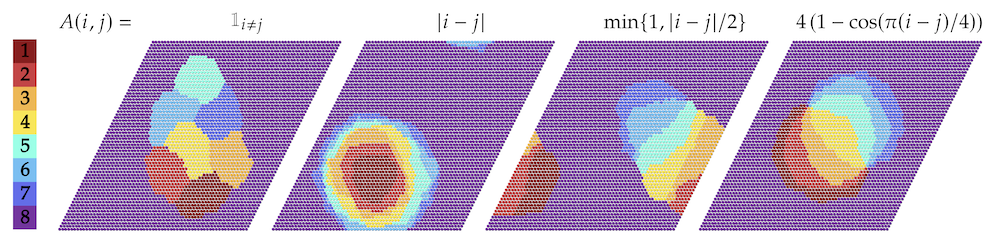
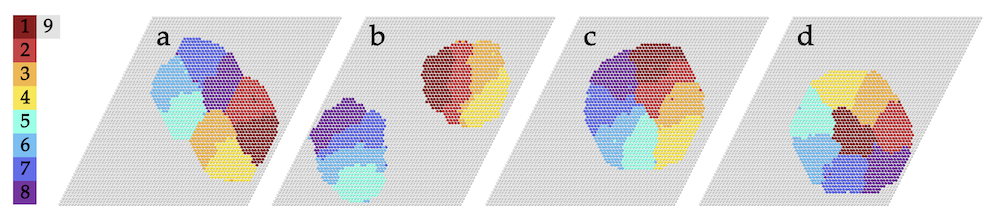
Connection to equilibrium statistical mechanics 🔗

The goals of statistical mechanics and programmable matter are inverses. While the former seeks to understand the collective behavior that arises from the dynamics of constituents, the latter seeks to design constituents that produce a desired collective behavior. This relationship underlies an approach to programmable matter pioneered by Dana and Andréa Richa. The idea is that, if you can encode the collective behavior of interest in the Hamiltonian of a model of equilibrium statistical mechanics, then the Glauber dynamics of the corresponding Gibbs distribution can, in some instances, be converted into a stochastic distributed algorithm for that behavior.

Some interesting aspects of this approach:

• Proving the correctness of the algorithm is equivalent to proving that the collective behavior of interest occurs with high probability under the Gibbs distribution. This is why our preprint is all about analyzing a Gibbs distribution.
• The approach works when the Glauber dynamics is a “local” Markov chain, meaning that the dynamics at the level of entire configurations of matter can be translated into dynamics for the constituents of that matter. The process of realizing the Markov chain dynamics in the dynamics of the constituents is sometimes called “physical embodiment.”
• The Glauber dynamics satisfies detailed balance, but it is used to program the behavior of a nonequilibrium system. The configurational dynamics of the nonequilibrium system are simulating the moves of a reversible Markov chain.