Theorem 4 of “Collapse and diffusion in harmonic activation and transport” states that there is a universal constant $c>0$ such that, if $A$ is a subset of $\mathbb{Z}^2$ with $n \geq 1$ elements, then the harmonic measure of $x$ in $A$ is either zero or at least $\exp (-c n \log n)$. In other words, the least positive value of harmonic measure can be no smaller than exponential in $n \log n$. See this post for a definition of harmonic measure and an explanation of why this is an interesting quantity to study. The same paper conjectured an optimal lower bound of $\exp (-c n)$. In fact, this was recently proved by Cai, Kozma, Procaccia, and Zhang, who introduced the notion of vertex-removal stability to do so!
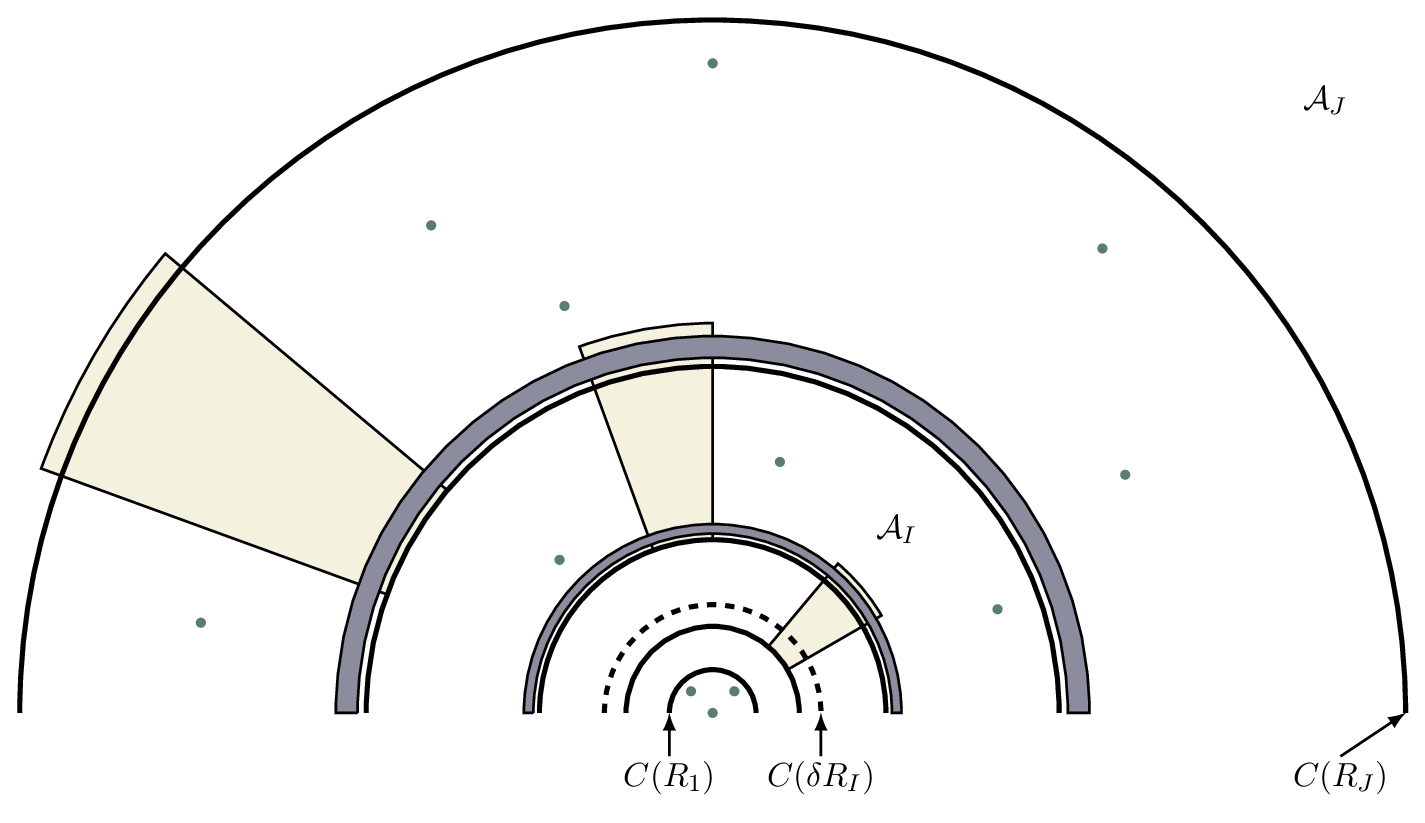
The proof of our estimate is by induction on $n$. The preceding figure illustrates a key idea in the induction step. Here, we assume (without loss of generality) that the origin has positive harmonic measure in $A$, and seek to bound below this harmonic measure.
To do so, we construct a contiguous sequence of radial (beige) and annular (blue) tunnels, through which a random walk starting in the outer annulus $\mathcal{A}_J$ can reach the inner circle $C(\delta R_I)$ without encountering the other elements of $A$ (green dots). I’ll spare you the definitions of $J$ and $I$, which label special annuli. Essentially, we use the induction hypothesis to advance random walk to the outer annulus, then tunnel to the inner circle, and use a separate estimate to reach the origin without hitting any other elements of $A$ within $C(R_1)$.
The fact that you can find such a sequence of tunnels to the origin follows from the pigeonhole principle applied to the radial and angular coordinates. The size of each tunnel depends on the number of elements of $A$ in the corresponding region, which affects how easily random walk navigates the tunnel, ultimately producing the $n$ dependence in our estimate. The argument requires quite a bit of notation, which the following, zoomed-in version provides.
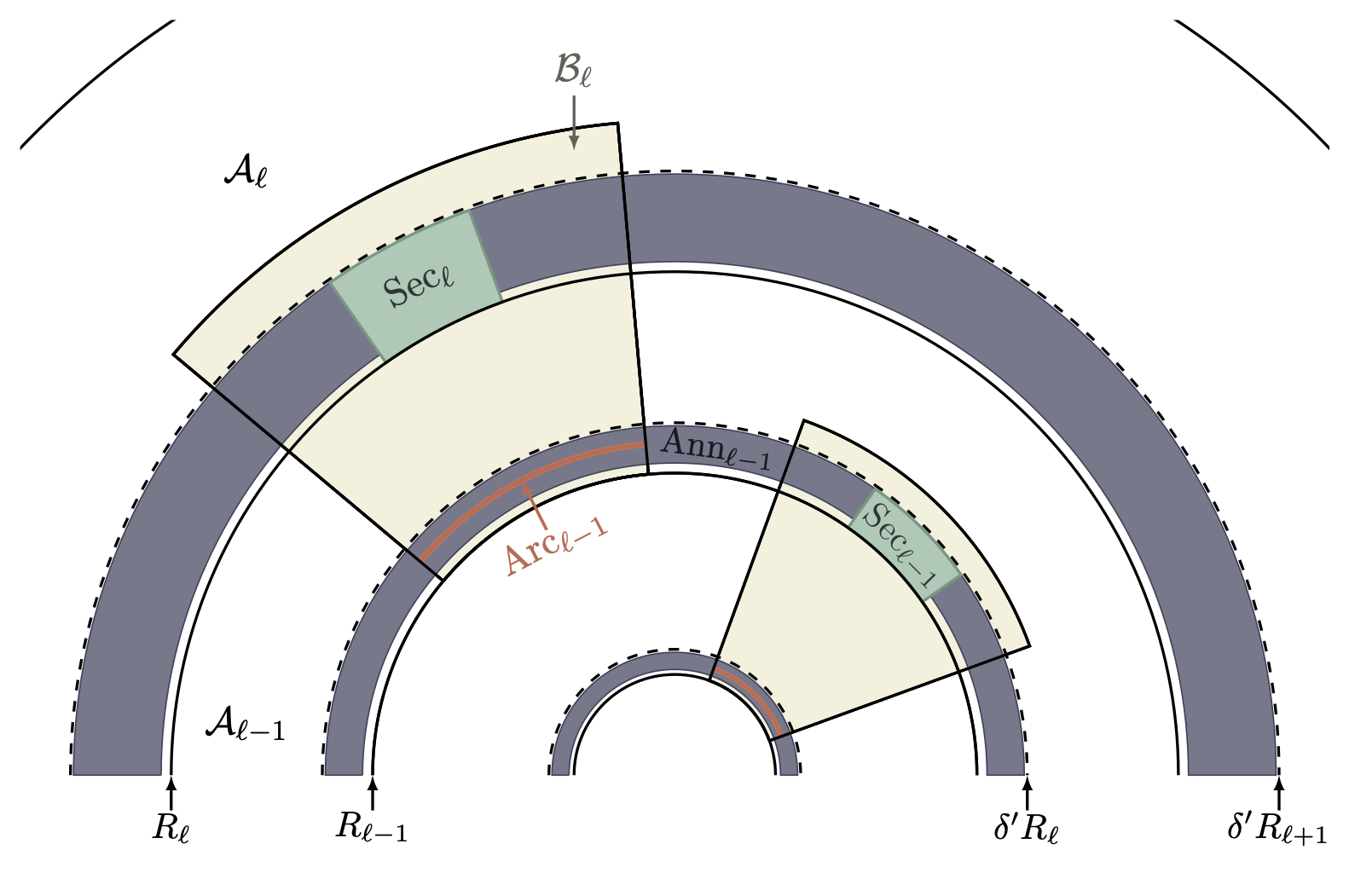
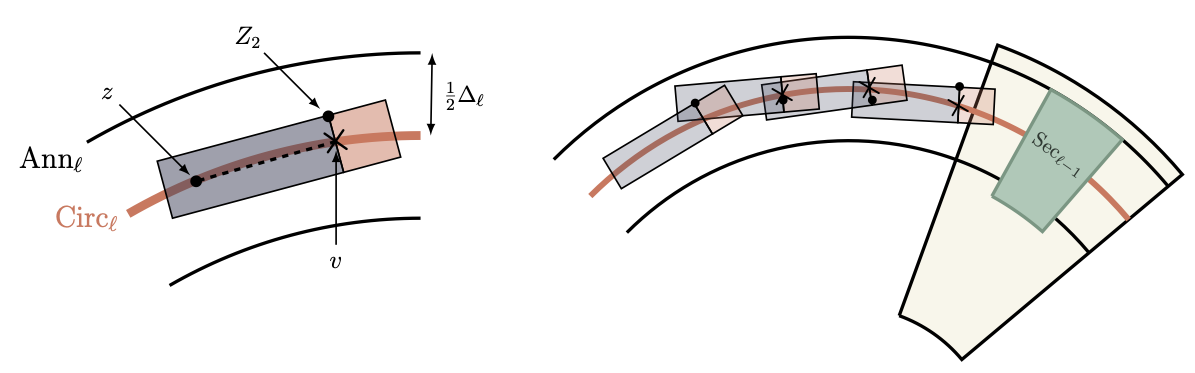
The random walk navigates each annular tunnel by exiting a sequence of rectangles through their far ends. The rectangles are situated along a guiding circle inside the annulus. The figure illustrating this didn’t make the paper, but I thought I’d include it anyway.
The .tex files that I used to generate these figures are linked in order above.