The paper “A local–global principle for nonequilibrium steady states” explains striking, recent experiments in active matter physics using Markov chain theory. To do so, the paper introduces the correlation coefficient
$$\rho = \mathrm{Corr}(-\log \pi (X), \log q(X)),$$where $\pi$ is the stationary distribution of an (irreducible) Markov chain on a finite state space, $q(x)$ is the sum of transition rates out of state $x$, and $X$ is a state chosen randomly according to some distribution. (By $\mathrm{Corr}(U,V)$, I mean the familiar Pearson correlation coefficient, defined by normalizing the covariance of $U$ and $V$.)
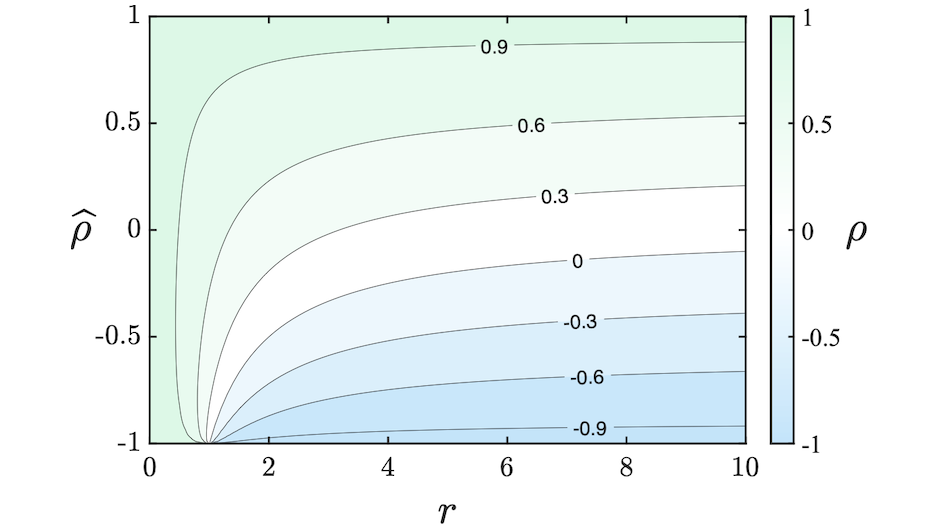
A key result of the paper is a simple formula for $\rho$ in terms of two other quantities $\widehat\rho$ and $r$, which together characterize the relationship between the local and global “parts” of $\pi$, in a sense that the paper details. Because the formula appears complicated, we visualized it using a contour diagram on the $(r,\widehat\rho)$ “strip.” I say strip because $\widehat\rho$ is also a correlation coefficient, so it takes values in the interval $[-1,1]$, while $r$ is a nonnegative number.
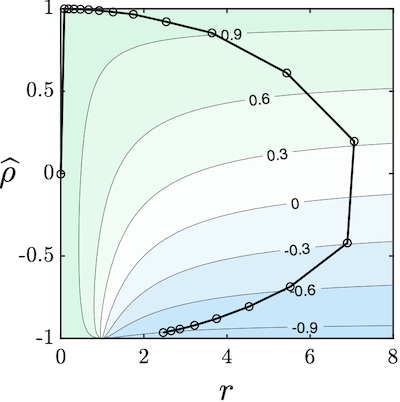
An interesting thing about these contour diagrams is that you can use them to visualize how local–global relationships change as the parameters of a Markov chain vary. For each value of the parameter, you plot a point on the strip—that is, each point corresponds to a Markov chain. Below is an example of dynamics of the Sherrington–Kirkpatrick spin glass from “Correlation thresholds in the steady states of particle systems and spin glasses.” It shows that, as a certain parameter of the Glauber dynamics varies, there is a rapid change from $\rho \approx -1$ (blue) to $\rho \approx 1$ (green), driven primarily by a change in $\widehat\rho$. Interpreting this threshold requires some discussion of what $\widehat\rho$ and $r$ represent. I’ll defer to the linked papers for that.